ODE Solvers with PINNs and shenanigans

Damped Oscillator!

Why this post exists

So I've been meaning to kind of branch out in machine learning, been stuck on building neural networks to predict stocks for too long! I was partly given this idea by Machine Learning 4 Science in their recent Google Summer of Code project that I hope to complete this summer!

I ended up falling down the rabbit hole of ODEs (ordinary differential equations) and got my top knocked off. I didn't really understand how to approach a single question; but my neural net might.. So I researched about PINNs, a kind of neural network specializing in math computations and everything physics!

This was something a lot more familiar to me given my background in ML, and I figured this was pretty neat so I wanted to document what I learned.

What I tried

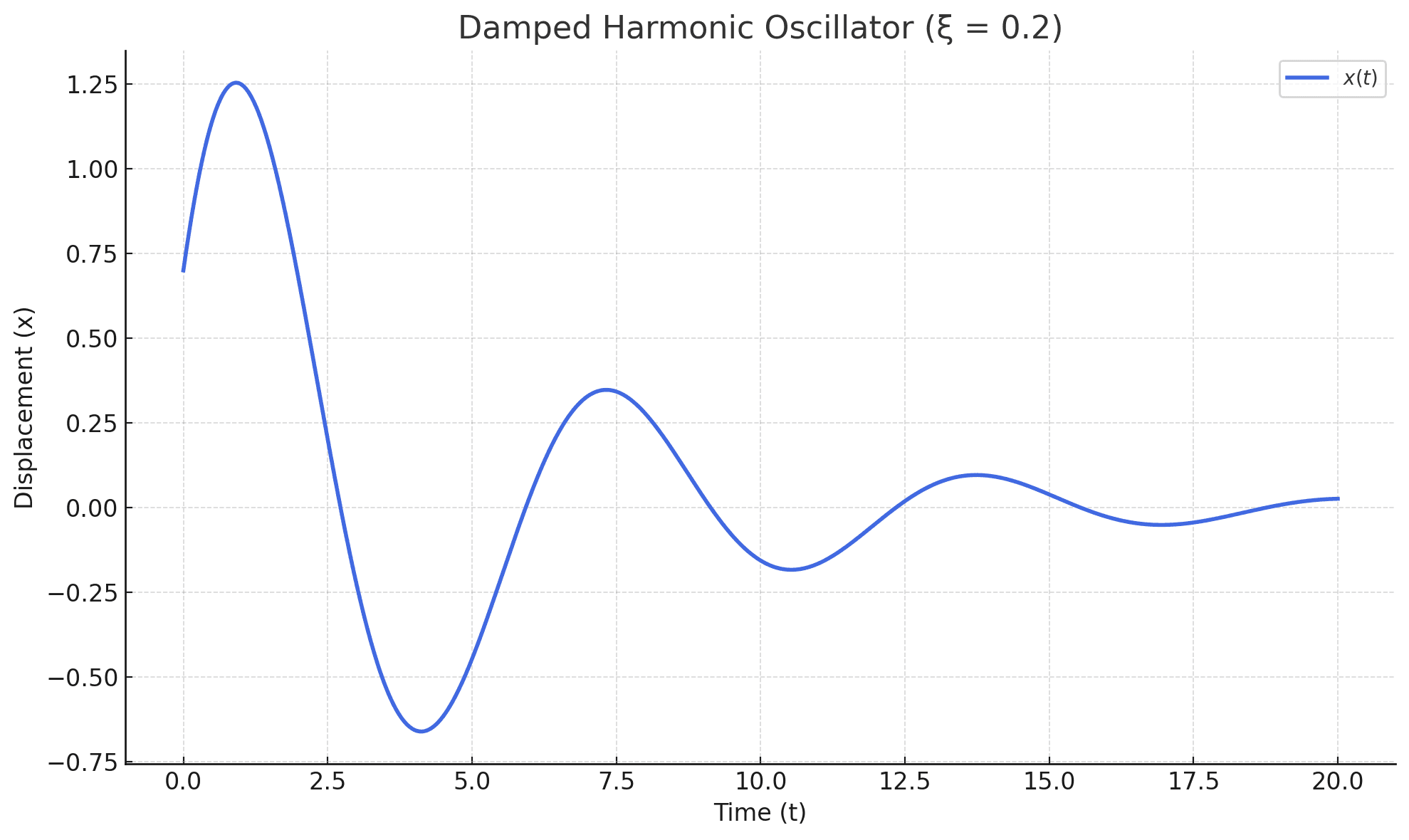
To start simple, I mainly focused on solving the damped harmonic oscillator - an alleged "classic" second-order ODE:

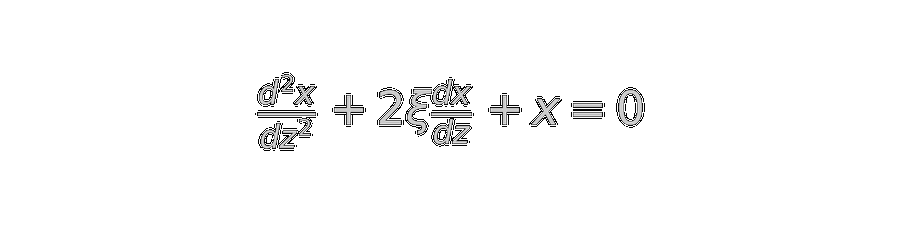
with initial conditions:

x(0) = 0.7
dx/dz(0) = 1.2

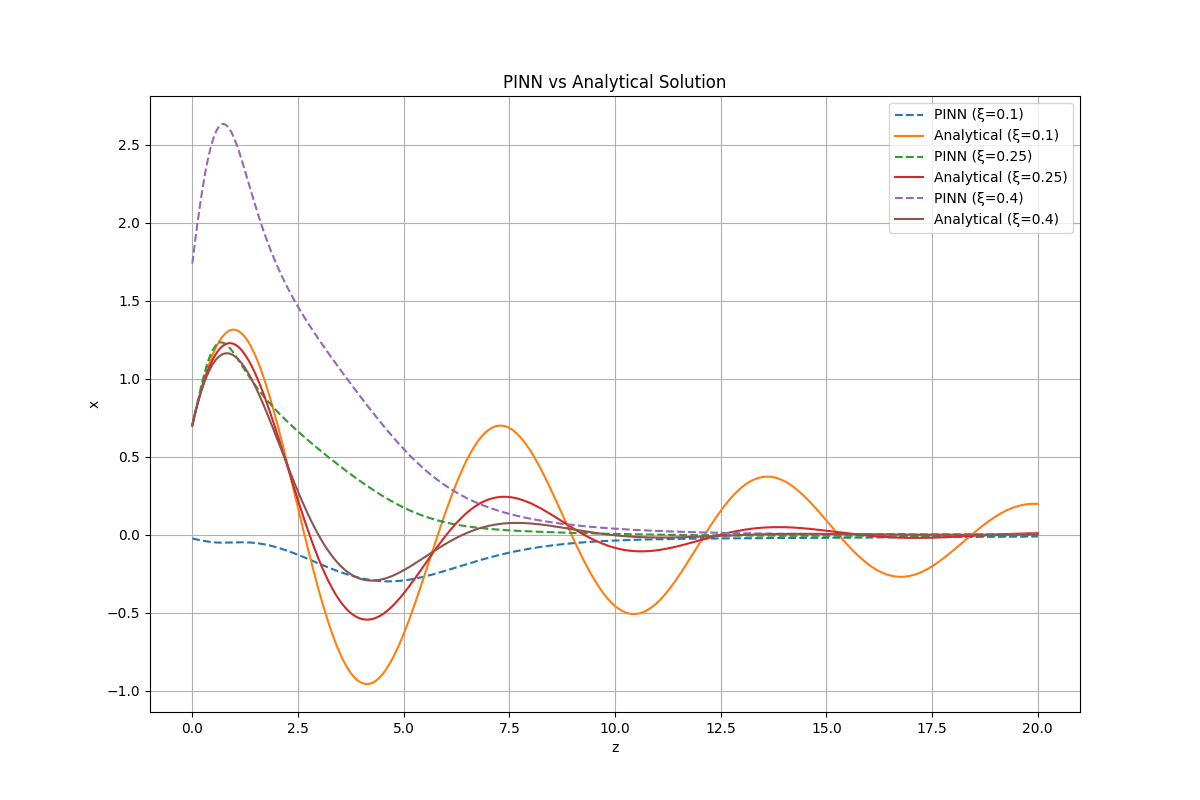
I focused on exploring a big range of damping ratios mainly from xi = 0.1 to 0.4, across the domain z in [0, 20].

This provided a great testbed for experimenting with PINNs with PyTorch. My goal was to train a neural net that satisfied the equation itself. Rather than matching some type of data; a fundamentally different paradigm from typical supervised learning.

Here's a simplified example of how I implemented the neural network:

import torch
import torch.nn as nn

class PINN(nn.Module):
    def __init__(self, hidden_dim=20):
        super(PINN, self).__init__()
        self.net = nn.Sequential(
            nn.Linear(1, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, 1)
        )
    
    def forward(self, z):
        return self.net(z)
        
    def compute_loss(self, z, xi=0.2):
        # Forward pass to get our predicted x
        z.requires_grad = True
        x = self(z)
        
        # Calculate derivatives using autograd
        dx_dz = torch.autograd.grad(
            x, z, grad_outputs=torch.ones_like(x),
            create_graph=True, retain_graph=True
        )[0]
        
        d2x_dz2 = torch.autograd.grad(
            dx_dz, z, grad_outputs=torch.ones_like(dx_dz),
            create_graph=True, retain_graph=True
        )[0]
        
        # ODE residual: d2x/dz2 + 2*xi*dx/dz + x = 0
        ode_residual = d2x_dz2 + 2*xi*dx_dz + x
        
        return torch.mean(ode_residual**2)

What I learned

I never knew that models can be trained to obey some set of rules instead of just fitting a dataset so that was cool, I also learned what a Residual was? and realized that the loss function was framed after the residual of my diffeq?

Also finally realized the importance of autograds! I mainly used my autograd for backprop in my own library, but with a PINN you're meant to use it to actually compute derivatives, big shocker for an automatic differentiator. There's also a whole charade about loss scaling that was a bit funky to wrap my head around.

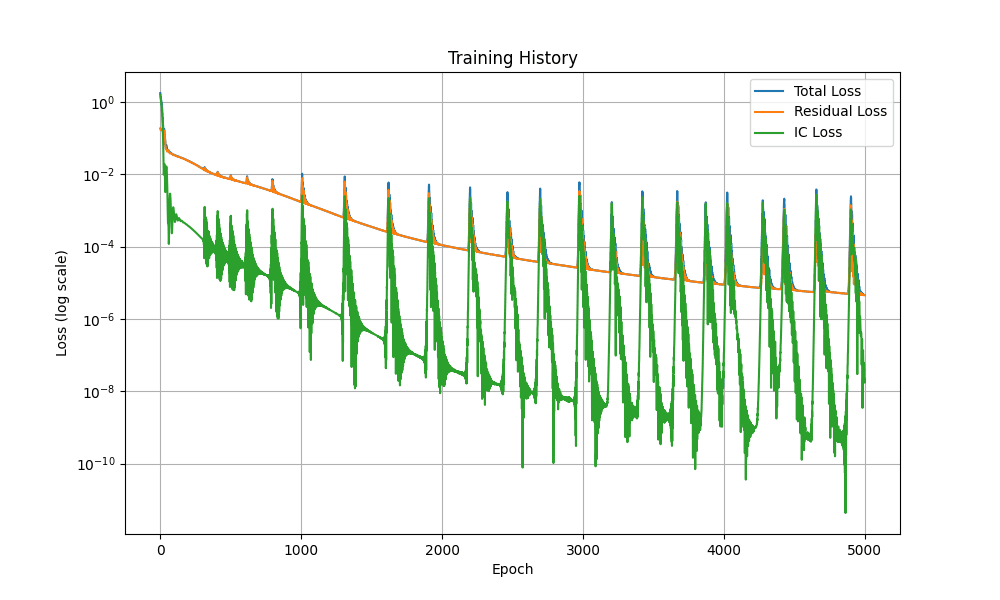
Sidenote: PINNs take FOREVER to train, genuinely ages. I tried deploying a LBFGS optimzer, and even tried curriculum training but nonetheless, it was a nightmare.

Loss function

I modeled the loss as:

ODE Residual - Using automatic differentiation (torch.autograd.grad) to get the first and second derivations of our predicted x(z)
Initial Condition Penalties - Adding parameters to ensure the net obeyed x(0) = 0.7 and x'(0) = 1.2

This essentially forced the net to obey physics directly

Results!

So, big shocker, the PINN actually learned the behavior of our oscillator pretty accurately. Check out the figure below this for a plot of our predicted solution vs. the analytical one (I used scipy for validation.)

The hard parts...

Getting my gradients right was so stupidly hard at first. I kept forgetting to retain my computational graph and got a stupid amount of RuntimeError's. (oops)
The network was super sensitive to weight initialization and learning rate, ugh.
I needed so much compute for this I nearly overworked my poor macbook air to death, I realized that this approach would probably scale much better when amortized over a bunch of queries (like sampling from a learned distribution.)

Where this is going

This project niceley tied in with a potential GSoC project, that I hope to work on where PINNs are used to model reverse-time diffusion equations for sampling from complex densities.

I'm hoping to try solving systems of ODE's next (maybe coupled oscillators or something?) and explore 3D inputs! Maybe I could model a PINN to solve a PDE like the heat equation in space and time? (Super stoked to tackle this.)

Now that I've kind of wrapped my head around PINNs, I'm hoping to see how they might train on more abstract domains like probability densities and what not.

Here's a link to the repo with the whole implementation bit: Github

Thanks for reading! Cya~

Vic